Traitement de signal¶

Cette partie du cours aborde les notions basiques sur:

Ce qu’est un signal.
Les conséquences de son enregistrement dans un format numérique.
L’analyse fréquentielle de son contenu.

Les points abordés ici sont détaillés plus finement dans le cours: Traitement_Signal_slides.pdf

Signal¶

Un signal undimensionnel peut être vu comme une fonction mathématique du type:

\[x: \; t \mapsto x(t)\]

Le signal sera périodique si il existe une période \(T\) telle que:

\[\forall t, \; x(t + T) = x(t)\]

On définit alors sa fréquence \(f = 1/T\). Dans le cas général, un signal quelconque pourra toujours être vu comme une somme de plusieurs signaux (ou composantes) périodiques.

Observation du signal¶

Pour des raisons pratiques, il est impossible d’observer un signal pour toutes les valeur de \(t\). On observe donc uniquement le signal entre \(t_0\) et \(t_1\). On définit alors la durée d’observation \(D = t_1 -t_0\).

Echantillonnage¶

Principe¶

Pour enregistre un signal dans un format numérique, on mesure ses valeurs sur une grille de points \([t_i]\) avec \(i \in [0, N-1]\), c’est l’échantillonnage. On enregistre donc \(N\) valeurs. Une grande quantité d’information est donc perdue par ce procédé. On définit aussi la fréquence d’échantillonnage:

\[f_e = \frac{N-1}{D}\]

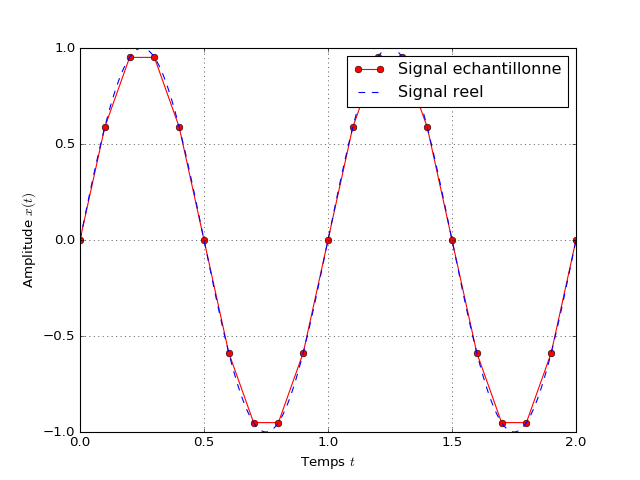
Dans l’exemple ci-dessous, les pastilles rouges représentent les points pour lesquelles les valeurs du signal réel sont enregistrées. On remarque les pastilles rouges décrivent bien la forme du signal réel, l’échantillonnage est donc réussi.

import numpy as np
import matplotlib.pyplot as plt

# Signal
T = 1.
def signal(t): return np.sin(2. * np.pi * t / T)
# Echantillonnage
D = 2. # Duree d'observation
fe = 10. # Frequence d'echantillonnage
N = int(D * fe) + 1 # Nombre de points enregistres
te = np.linspace(0., (N-1)/fe, N) # Grille d'echantillonnage
tp = np.linspace(0., D, 1000) # Grille plus fine pour tracer l'allure du signal parfait
# Trace du signal
plt.plot(te, signal(te), 'or-', label = u"Signal echantillonne")
plt.plot(tp, signal(tp), 'b--', label = u"Signal reel")
plt.grid()
plt.xlabel("Temps $t$")
plt.ylabel("Amplitude $x(t)$")
plt.legend()
plt.show()

(Source code, png, hires.png, pdf)

Théorème de Shannon-Nyquist¶

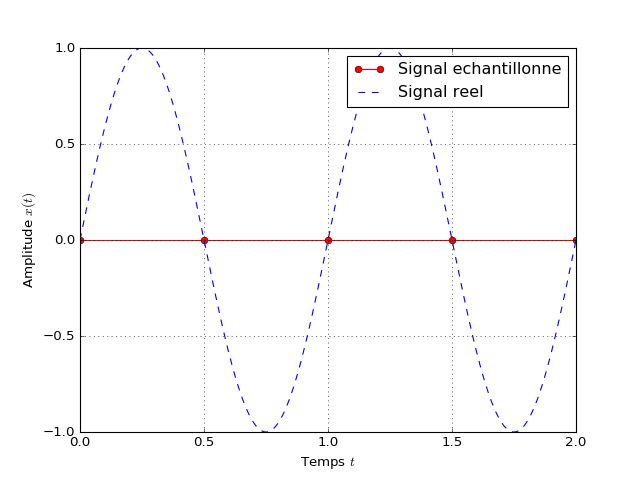
Le théorème de Shannon Nyquist indique que la fréquence \(f\) du signal (ou celles de ses composantes) doit vérifier:

\[f < \frac{f_e}{2}\]

Le cas extrême où \(f = f_e/2\) est représenté ci-dessous.

import numpy as np
import matplotlib.pyplot as plt

# Signal
T = 1.
def signal(t): return np.sin(2. * np.pi * t / T)
# Echantillonnage
D = 2. # Duree d'observation
fe = 2. # Frequence d'echantillonnage
N = int(D * fe) + 1 # Nombre de points enregistres
te = np.linspace(0., D, N) # Grille d'echantillonnage
tp = np.linspace(0., D, 1000) # Grille plus fine pour tracer l'allure du signal parfait
# Trace du signal
plt.plot(te, signal(te), 'or-', label = u"Signal echantillonne")
plt.plot(tp, signal(tp), 'b--', label = u"Signal reel")
plt.grid()
plt.xlabel("Temps $t$")
plt.ylabel("Amplitude $x(t)$")
plt.legend()
plt.show()

(Source code, png, hires.png, pdf)

Repliement de spectre¶

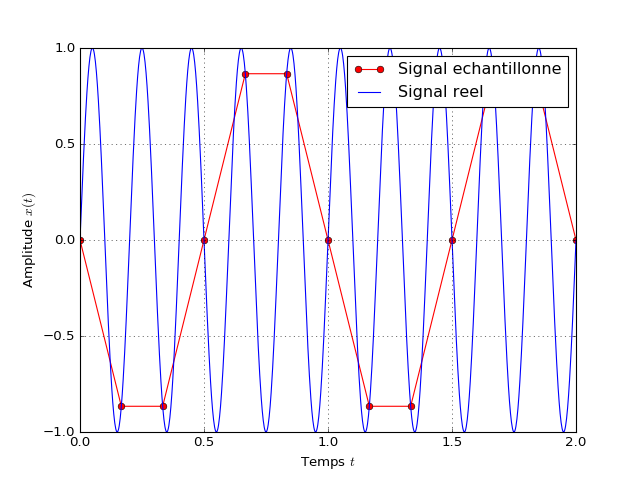
La figure ci-dessus laisse penser que si la fréquence du signal ne respecte pas le théorème de Shannon-Nyquist, alors le signal est perdu lors de l’échantillonnage. En réalité, le signal apparait comme ayant une fréquence différente comme le montre la figure ci-dessous.

import numpy as np
import matplotlib.pyplot as plt

# Signal
T = .2
def signal(t): return np.sin(2. * np.pi * t / T)
# Echantillonnage
D = 2. # Duree d'observation
fe = 6. # Frequence d'echantillonnage
N = int(D * fe) + 1 # Nombre de points enregistres
te = np.linspace(0., (N-1)/fe, N) # Grille d'echantillonnage
tp = np.linspace(0., D, 1000) # Grille plus fine pour tracer l'allure du signal parfait
# Trace du signal
plt.plot(te, signal(te), 'or-', label = u"Signal echantillonne")
plt.plot(tp, signal(tp), 'b-', label = u"Signal reel")
plt.grid()
plt.xlabel("Temps $t$")
plt.ylabel("Amplitude $x(t)$")
plt.legend()
plt.show()

(Source code, png, hires.png, pdf)

Pour échantillonner un signal, il est donc essentiel de retirer préalablement les composantes de fréquence \(f \geq f_e/2\) à l’aide d’un filtre anti repliement.

Analyse Spectrale¶

Principe¶

L’ analyse spectrale d’un signal consiste à construire son spectre, c’est-à-dire sa décomposition sous forme d’une somme fonctions périodiques. Plusieurs outils existent selon le type de signal étudié. Dans la pratique, nous allons travaillons toujours avec des signaux apériodiques échantillonnés, l’outil de base de base pour construire le spectre est la Transformé de Fourier Discrète (DFT) ou son implémentation rapide, la FFT . En python, le moyen le plus simple pour accéder aux algorithmes de FFT est scipy . L’algorithem FFT impose que le nombre d’échantillon \(N\) soit une puissance de 2.

>>> N = len(x)
>>> fe = 1. / (t[1] - t[0])

Dans la pratique la FFT d’un signal \(x\) se présente de la manière suivante:

>>> from scipy import fftpack
>>>  X = fftpack.fft(x)

Le vecteur \(X\) est composé de \(N\) coefficients complexes. La première moitié des coefficients du vecteur \(X\) correspondent aux fréquences positives et la seconde aux fréquences négatives.

>>> Xpos = X[0:N/2] # Coefficients correspondant aux frequences positives
>>> Xneg = X[N/2:N] # Coefficients correspondant aux frequences negatives

Dans notre cas, le signal \(x\) étant réel, les coefficients correspondant aux fréquences négatives sont les conjugués des coefficients correspondant aux fréquences positives, ils n’apportent donc pas d’information utile.

Le vecteur fréquence \(f\) correspondant au vecteur \(X\) comporte \(N\) coefficients se répartissant entre \(-f_e/2\) et \(f_e/2\). Dans la pratique, il n’est pas intéressant de tracer les fréquences négatives, nous pouvons donc tracer un signal et son spectre de la manière suivante:

>>> f = np.linspace(0., fe/2., N/2)

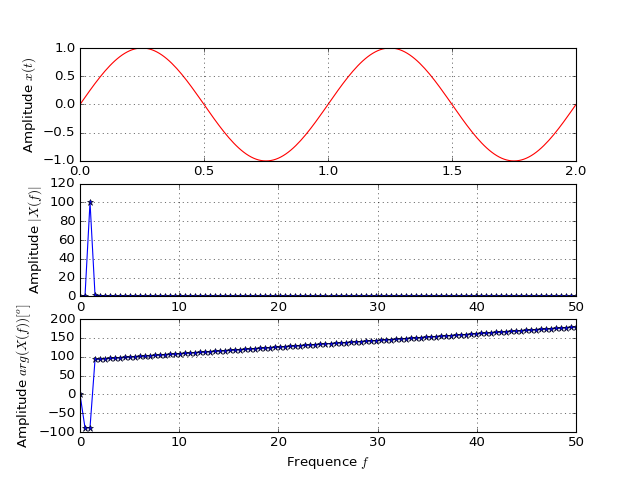
Mise en pratique:

import numpy as np
import matplotlib.pyplot as plt
from scipy import fftpack

# Signal
T = 1.
def signal(t): return np.sin(2. * np.pi * t / T)
# Echantillonnage
D = 2. # Duree d'observation
fe = 100. # Frequence d'echantillonnage
N = int(D * fe) + 1 # Nombre de points enregistres
t = np.linspace(0., (N-1)/fe, N) # Grille d'echantillonnage
x = signal(t)
# FFT
X = fftpack.fft(x)
fpos = np.linspace(0., fe/2., N/2)
Xpos = X[0:N/2]
# Trace du signal et de son spectre
fig = plt.figure(0)
ax = fig.add_subplot(3,1,1)
plt.plot(t, x, 'r-')
plt.grid()
plt.xlabel("Temps $t$")
plt.ylabel("Amplitude $x(t)$")
ax = fig.add_subplot(3,1,2)
plt.plot(fpos, abs(Xpos), 'b*-')
plt.grid()
plt.ylabel("Amplitude $|X(f)|$")
ax = fig.add_subplot(3,1,3)
plt.plot(fpos, np.degrees(np.angle(Xpos)), 'b*-')
plt.grid()
plt.xlabel("Frequence $f$")
plt.ylabel("Amplitude $arg(X(f)) [^o]$")
plt.show()

(Source code, png, hires.png, pdf)

Interprétation¶

Effet de la fréquence:

(Source code, png, hires.png, pdf)

Travaux dirigés¶

Ce sujet est une introduction aux questions abordées dans ce cours. On vous demande d’écrire un (ou plusieurs) scripts qui pour effectuer les tâches suivantes:

Signal sinusoidal

Générer un signal sinusoidal de la forme \(x(t) = a \sin (2 \pi f t + \phi)\).

Construire une grille d’échantillonnage \(t\) pour laquelle on peut contrôler la fréquence d’échantillonnage \(f_e\) et la durée d’observation \(D\).

Tracer le signal échantillonné.

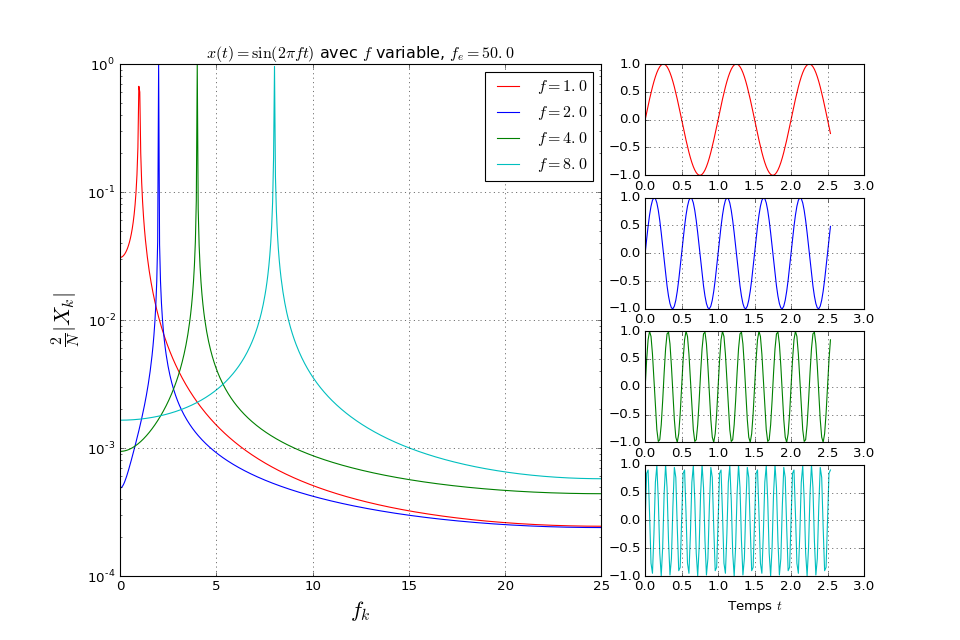
Que se passe-t-il quand on augmente la fréquence du signal \(f\) en laissant \(f_e\) constante.

Calculer la transfromée de Fourier par FFT \(X\) des coefficients \(x\).

Calculer les fréquences positives.

Tracer le spectre du signal.

Expliquer l’influence de \(a\) , \(f\) et \(\phi\) sur le spectre.

Autres signaux

Réutilisez le code produit dans les questions précédentes et appliquez le à un signal carré.

Même démarche pour un signal constant.

Même démarche pour une gaussienne.

Travaux Pratiques¶

Signaux

On a en enregistré deux signaux expérimentaux au moyen d’un accéléromètre:

Un signal enregistré par un accéléromètre sur une cloche: cloche.txt.
Un signal enregistré sur une poutre que l’on met en vibration au moyen d’un marteau de choc: poutre_Al_flexion.txt.

Etude de la poutre

La poutre est constituée d’un alliage d’aluminium. Elle est de forme parallélépipédique de longueur \(l = 600 \; mm\), de hauteur de \(h = 15 \; mm\) et de largeur de \(b = 30 \; mm\). La masse volumique est mesurée préalablement est vaut \(\rho = 2700 \; kg/m^3\). Elle est sollicitée de manière à vibrer en flexion. D’un point de vue théorique, une poutre sollicité en flexion va présenter plusieurs modes propres correspondant chacun à une fréquence propre \(f_n\) vérifiant:

\[f_n = \frac{1}{2\pi}\frac{C_n^2}{l^2}\sqrt{\frac{E}{\rho}} \sqrt{ \frac{I}{S} }\]

Avec:

\(I\): le moment quadratique de la section qui vaut: \(b h^3 / 12\).
\(S\): l’aire de la section de la poutre qui vaut \(b h\) .
\(C_n\): un coefficient qui dépent du numéro \(n\): du mode considéré.

On donne:

\(n\)	\(C_n^2\)
1	22.37
2	61.67
>2	\(((2n + 1)\pi/2)^2\)

Travail demandé: écrire un script Python qui effectue les tâches suivantes:

Tracer le signal de l’accélération en fonction du temps.

Calculer le spectre de l’accélération par FFT.

Tracer le module du spectre \(|X|\):.

Identifier automatiquement les modes propres de la poutre.

Déterminer le module du Young \(E\): de l’alliage utilisé.

Etude de la cloche.

La cloche est prévue pour sonner le Ré, implique de produire certaines fréquences particulières

Composante	Formule	Valeur
Hum	\(f_0\)	276.8 Hz
Fondamentale	\(2f_0\)	553.6 Hz
Tierce	\(2.4f_0\)	664.3 Hz
Quinte	\(3f_0\)	830.4 Hz
Octave	\(4f_0\)	1107 Hz

Travail demandé: écrire un script Python qui effectue les tâches suivantes. Pour ce faire vous pouvez grandement réutiliser les outils développés dans la partie précédente:

Tracer le signal de l’accélération en fonction du temps.

Calculer le spectre de l’accélération par FFT.

Tracer le module du spectre \(|X|\) .

Identifier automatiquement les différentes harmoniques présentes dans le signal.

Déterminer le niveau d’erreur sur chaque harmonique.